El problema
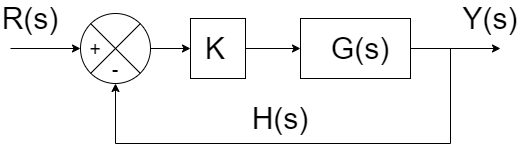
\(fig.\;1\)
a) Encontrar la función de transferencia en lazo cerrado.
b) Realizar la tabla de Routh.
c) Determinar el rango de \(k\) para que el sistema sea estable.
d) Validar gráficamente los resultados usando la función step en Matlab.
Inciso a
Encontrar la función de transferencia en lazo cerrado
En este caso tenemos la función de transferencia en este sistema que es:
$$G(s)=\frac{1}{s(s^2+2s+3)(s+4)}\tag{1.1}$$
Es bueno tener en mente que esta función, ya cuando se expande el denominador, se vuelve:
$$G(s)=\frac{1}{s^4+6s^3+11s^2+12s}\tag{1.1a}$$
Ocupamos encontrar la función de transferencia en lazo cerrado que la vamos a denominar \(T(s)\) y por definición sabemos que:
$$T(s)=\frac{Y(s)}{R(s)}=\frac{G(s)}{1+G(s)H(s)}\tag{1.2}$$
Importante recordar que la \(G(s)\) mencionada en \((1.2)\) no es la misma \(G(s)\) de \((1.1)\). La \(G(s)\) de \((1.2)\) es la función de transferencia del sistema de \((1.1)\) afectada por la entrada escalonada \(k\). En otras palabras la \(G(s)\) de \((1.2)\) es la \(fig.\;2\) mostrada abajo:
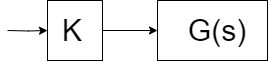
\(fig.\;2\)
Para no confundirnos, vamos a nombrar una nueva función de transferencia que considera la \(k\) y la nombraremos \(G_{1}(s)\), de tal manera que:
$$G_{1}(s)=k*G(s)=\frac{k}{s(s^2+2s+3)(s+4)}\tag{1.3}$$
Y entonces con esta nueva definición reescribimos la ecuación de la función de transferencia de lazo cerrado que ocupamos encontrar:
$$T(s)=\frac{Y(s)}{R(s)}=\frac{G_{1}(s)}{1+G_{1}(s)H(s)}\tag{1.4}$$
Ahora sí, para resolver este problema vamos a sustituir valores en la \((1.4)\). Para esto pondremos que \(H(s)=1\) ya que estamos considerando que la respuesta es instantanea (no es exactamente cierto, pero es bueno para aproximar). Y entonces tenemos:
$$T(s)=\frac{G_{1}(s)}{1+G_{1}(s)H(s)}=\frac{\frac{k}{s(s^2+2s+3)(s+4)}}{1+\frac{k}{s(s^2+2s+3)(s+4)}(1)}\tag{1.5}$$
De aquí, en el denominador \(1+\frac{k}{s(s^2+2s+3)(s+4)}(1)\), el \(1\) que se está sumando lo convertimos en \(\frac{s(s^2+2s+3)(s+4)}{s(s^2+2s+3)(s+4)}\) para poder sumarlo con \(\frac{k}{s(s^2+2s+3)(s+4)}\) (aquí ya no ponemos el \(1\) ya que cualquier valor multiplicado por \(1\) queda igual) y entonces nos queda:
$$T(s)=\frac{\frac{k}{s(s^2+2s+3)(s+4)}}{\frac{s(s^2+2s+3)(s+4)+k}{s(s^2+2s+3)(s+4)}}\tag{1.6}$$
Para resolver esto usamos lo que se denomina como la ley de la herradura y nos queda así:
$$\eqalign{T(s)&=\frac{\frac{k}{s(s^2+2s+3)(s+4)}}{\frac{s(s^2+2s+3)(s+4)+k}{s(s^2+2s+3)(s+4)}}\\&= \frac{k}{s(s^2+2s+3)(s+4)}*\frac{s(s^2+2s+3)(s+4)}{s(s^2+2s+3)(s+4)+k}}$$
Al simplificar un poco esto, nos queda:
$$T(s)=\frac{k}{s(s^2+2s+3)(s+4)+k}\tag{1.7}$$
Pero para poder hacer la tabla de Routh ocupamos que todo esté desarrollado (sin factores). Y entonces tenemos:
$$T(s)=\frac{k}{s^4+6s^3+11s^2+12s+k}\tag{1.8}$$
Y cualquiera de las dos \((1.7)\) o \((1.8)\) sirven para lo que pide el inciso a.
Inciso b
Realizar la tabla de Routh
Para este inciso es necesario hacer la tabla de Routh. Para esto primero ocupamos ver el polinomio característico y revisar que todos los términos sean positivos y que no haya brincos en las potencias de \(s\).
Así como vimos en el inciso a anteriormente, el polinomio característico es el denominador de \((1.8)\):
$$s^4+6s^3+11s^2+12s+k\tag{1.9}$$
Viendo esta expresión podemos observar que todos los términos son positivos y que desde \(s^4\) hasta \(s^0\) no se salta ninguna potencia, así que estamos libres de seguir con la tabla de Routh.
Para hacer la tabla de Routh veamos el caso general para poder armarla. Teniendo un polinomio característico de la forma:
$$a_0s^n+a_1s^{n-1}+a_2s^{n-2}+…+a_{n-1}s^1+a_ns^0$$
Se desarrolla la siguiente tabla:
*nota: la primera columna son las potencias de \(s\) y las primeras dos filas y la ultima fila \(a_n\), que son los coeficientes, los obtenemos del polinomio característico.
$$s^n$$ |
$$a_0$$ |
$$a_2$$ |
$$a_4$$ |
$$a_6$$ |
... |
$$s^{n-1}$$ |
$$a_1$$ |
$$a_3$$ |
$$a_5$$ |
$$a_7$$ |
... |
$$s^{n-2}$$ |
$$b_1=\frac{a_1a_2-a_3a_0}{a_1}$$ |
$$b_2=\frac{a_1a_4-a_5a_0}{a_1}$$ |
$$b_3=\frac{a_1a_6-a_7a_0}{a_1}$$ |
... |
... |
$$s^{n-3}$$ |
$$c_1=\frac{b_1a_3-b_2a_1}{b_1}$$ |
$$c_2=\frac{b_1a_55-b_3a_1}{b_1}$$ |
$$\vdots$$ |
||
$$\vdots $$ |
$$\vdots$$ |
$$\vdots$$ |
$$\vdots$$ |
||
$$s^1$$ |
$$\vdots$$ |
$$\vdots$$ |
|||
$$s^0$$ |
$$a_n$$ |
\(tabla\;1\)
Teniendo esta tabla podemos tomar los valores necesarios de nuestro polinomio caracteríco y armar nuestra propia tabla. Haciendo las equivalencias tenemos:
$$\eqalign{s^n&=s^4\\s^{n-1}&=s^3\\s^{n-2}&=s^2\\s^1&=s^1\\s^0&=s^0}\qquad\eqalign{a_0&=1\\a_2&=11\\a_4&=k\\a_1&=6\\a_3&=12\\a_n&=k}$$
Teniendo estos valores vamos a rellenar parcialmente la tabla de Routh de nuestro problema:
*nota: como podemos ver, no hay un valor \(a_5\) así que se rellena con un \(0\) para que las primeras dos filas tengan la misma longitud
$$s^4$$ |
$$1$$ |
$$11$$ |
$$k$$ |
$$s^3$$ |
$$6$$ |
$$12$$ |
$$0$$ |
$$s^2$$ |
$$b_1$$ |
$$b_2$$ |
|
$$s^1$$ |
$$c_1$$ |
||
$$s^0$$ |
$$k$$ |
\(tabla\;2\text{ – tabla de Routh parcial de acuerdo a nuestro problema}\)
Como podemos ver, ya están casi todos los valores rellenos de la tabla excepto por \(b_1, b_2\) y \(c_1\). Estando las cosas así, veremos a la \(tabla\;1\) para poder encontar los valores deseados. Para encontrar los valores se ocupa de una determinante negativa. Así que simplemente sustituimos valores y resolvemos.
Así que, para encontrar el valor \(b_1\):
$$\eqalign{b_1&=\frac{a_1a_2-a_3a_0}{a_1}\\&=\frac{(6)(11)-(12)(1)}{6}\\&=\frac{54}{6}\\&=9}$$
De igual manera resolvemos para el valor \(b_2\):
$$\eqalign{b_2&=\frac{a_1a_4-a_5a_0}{a_1}\\&=\frac{(6)(k)-(0)(1)}{6}\\&=k}$$
Y finalmente resolvemos para \(c_1\) para así poder tener todos los valores de la segunda columna de la tabla (que es lo que buscamos):
$$\eqalign{c_1&=\frac{b_1a_3-b_2a_1}{b_1}\\&=\frac{(9)(12)-(6)(k)}{9}\\&=\frac{108-6k}{9}}$$
Ahora sí, teniendo todos los valores, los sustituimos a la tabla y terminamos con este inciso:
$$s^4$$ |
$$1$$ |
$$11$$ |
$$k$$ |
$$s^3$$ |
$$6$$ |
$$12$$ |
$$0$$ |
$$s^2$$ |
$$9$$ |
$$k$$ |
|
$$s^1$$ |
$$\frac{108-6k}{9}$$ |
||
$$s^0$$ |
$$k$$ |
\(tabla\;3\text{ – tabla de Routh para este problema}\)
Inciso c
Determinar el rango de \(k\) para que el sistema sea estable
Como ya habiamos mencionado, uno de los criterios que se necesitan para saber si un sistema es estable es que los coeficientes del polinomio característico sean positivos y el otro es que la segunda columna tenga todos los valores positivos. Al observar podemos notar que los primeros tres valores son positivos, pero el cuarto y quinto valor son variables porque \(k\) está incluido.
Primer valor |
$$1$$ |
Segundo valor |
$$6$$ |
Tercer valor |
$$9$$ |
Cuarto valor |
$$\frac{108-6k}{9}$$ |
Quinto valor |
$$k$$ |
\(tabla\;4\text{ – valores de la segunda columna}\)
Considerando esto, entonces debemos encontrar los rangos de \(k\) de tal manera que el cuarto y quinto valor sean positivos. Eso quiere decir que las siguientes condiciones tienen que cumplirse:
$$\frac{108-6k}{9}>0\tag{1.10}$$
y
$$k>0\tag{1.11}$$
Para la \((1.11)\) no hay mucho problema, \(k\) solo tiene que ser mayor a \(0\). El problema es con la \((1.10)\) que se necesita resolver para ver que valores de \(k\) ocupamos para mantener el cuarto valor positivo.
Entonces resolviendo:
$$\eqalign{\frac{108-6k}{9}&>0\\108-6k&>0\\-6k&>-108\\6k&<108\\k&<18}$$
Habiendo resuelto esto entonces tenemos que:
$$0<k<18$$
O sea, el valor de \(k\) debe ser entre \(0\) y \(18\).
Inciso d
Validar gráficamente los resultados usando la función step en Matlab
Lo que sigue ahora es validar que los valores que encontramos de \(k\) son en realidad los que mantienen estable esta función de transferencia en lazo cerrado. Para esto usamos Matlab y abrimos un nuevo script con el siguiente código:
*nota: si no saben usar bien Matlab, vean el video al inicio de este artículo a partir del minuto 16:00. O dale clic aquí
k = 0;
num = 1;
den = [1 6 11 12 0];
Gs = tf(num,den);
Gs1 = k*Gs;
Ts = feedback(Gs1,1);
step(Ts);
Explicando las líneas de código arriba:
En la primera línea definimos la variable k igual a \(0\) pero este valor lo podemos cambiar como queramos.
En la segunda línea definimos la variable num igual a \(1\) y este es el valor del numerador de la función de transferencia original, antes de aplicar la k, revisar la \((1.1)\).
En la tercera línea definimos la variable den y la igualamos a con los valores \(1\;6\;11\;12\;0\) dentro de \([\;]\) para que en automático Matlab haga el polinomio que se encuentra en el denomiador de la \((1.1)\) pero expandida y no en factores, o sea como en el denominador de la \((1.1a)\). En otras palabras para que sea lo mismo a:
$$s(s^2+2s+3)(s+4)=s^4+6s^3+11s^2+12s+0$$
En la cuarta línea definimos la variable Gs y aquí es donde guardamos la función de transferencia original \((1.1)\) usando la función interna de Matlab, tf.
En la quinta línea definimos la variable Gs1 donde guardamos la función de transferencia original \((1.1)\) afectada por la k, o sea la \((1.3)\).
En la sexta línea definimos la variable Ts donde se guarda la función en lazo cerrado creada usando una función interna de Matlab, feedback .
En la séptima línea creamos la gráfica de la función en lazo cerrado usando la función interna step de Matlab que hace una gráfica del tipo de entrada step.
Sabiendo que el rango de \(k\) debe ser entre 0 y 18, hagamos unas gráficas en Matlab usando step con diferentes valores de k para ver los resultados y validar que sí estamos en lo correcto.
Abajo veremos como se comportan las gráficas con los diferentes valores.
Utilizaremos los siguientes valores de k: 0, 1, 5, 16, 17, 18 y 18.1.
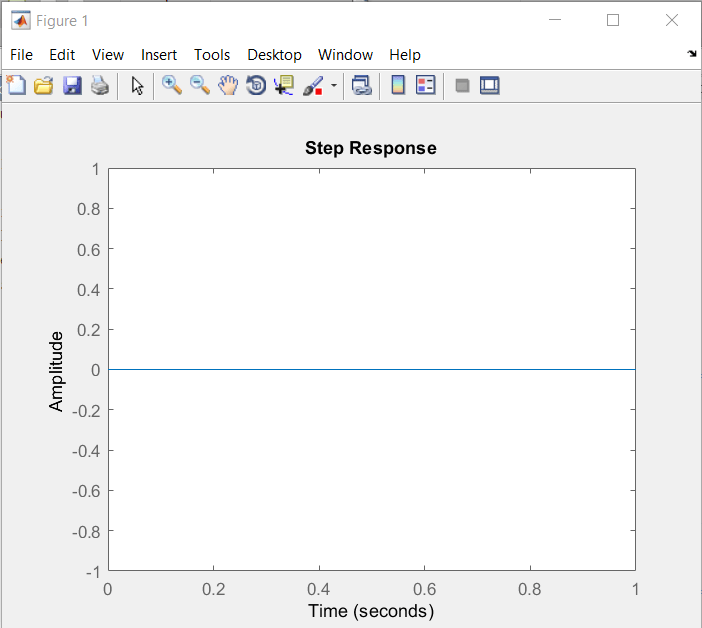
\(fig.\;3\)
En la \(fig.\;3\) podemos ver la gráfica cuando la entrada k es de 0. Es precisamente como esperamos, no hay respuesta.
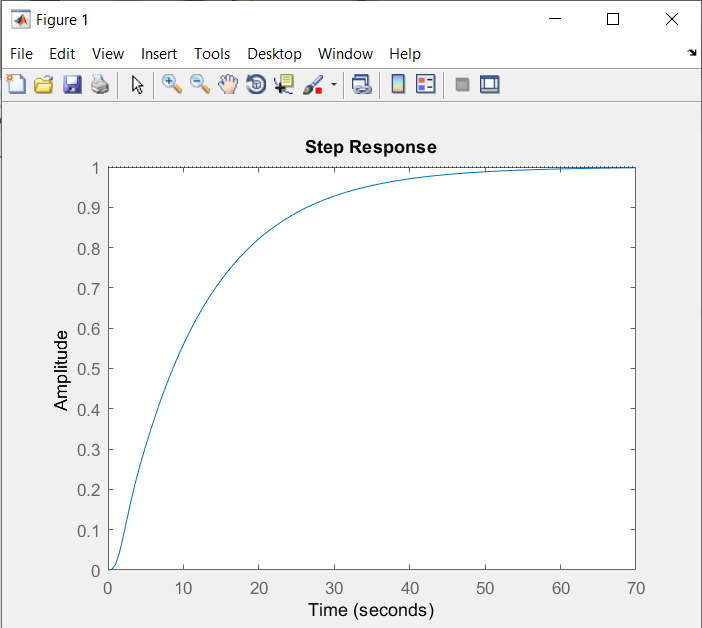
\(fig.\;4\)
En la \(fig.\;4\) podemos ver la gráfica cuando la entrada k es de 1. Como podemos ver en la respuesta, si alcanza a estabilizarse aunque toma unos 70 segundos.
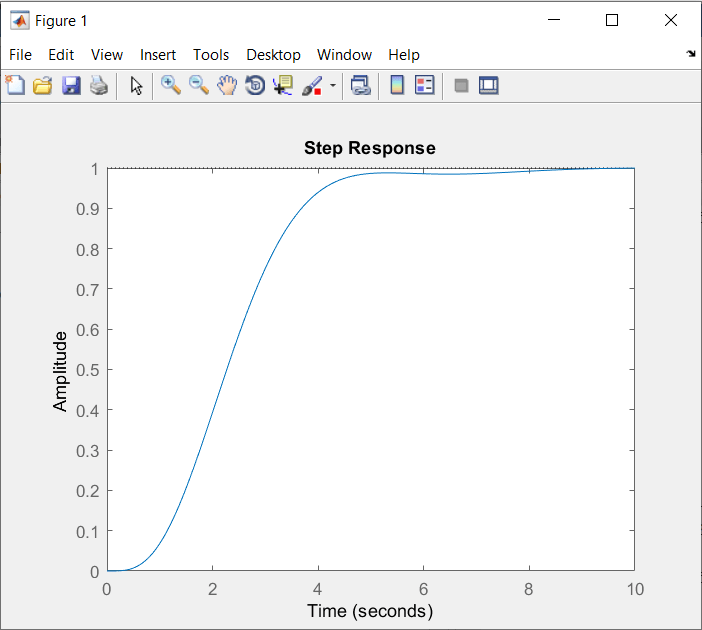
\(fig.\;5\)
En la \(fig.\;5\) podemos ver la gráfica cuando la entrada k es de 5. Como podemos ver en la respuesta, si alcanza a estabilizarse con un muy ligera oscilación y solo tarda como 10 segundos.
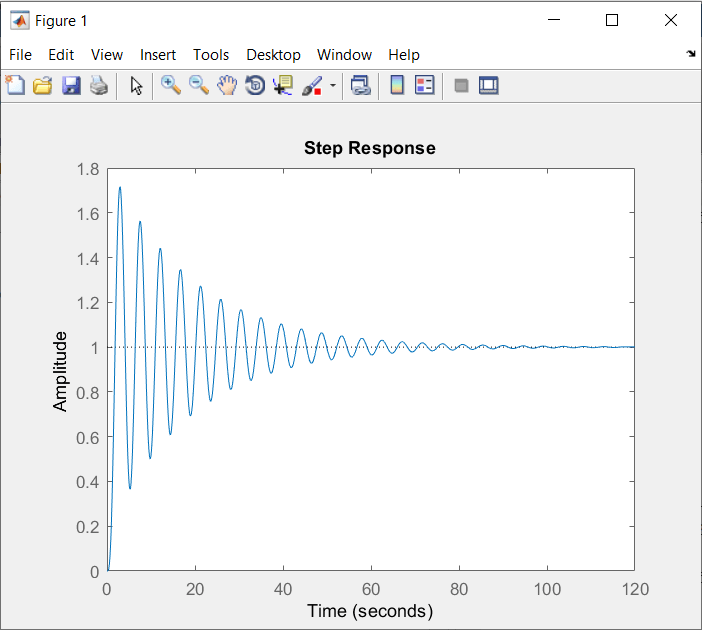
\(fig.\;6\)
En la \(fig.\;6\) podemos ver la gráfica cuando la entrada k es de 16. Como podemos ver en la respuesta, si alcanza a estabilizarse con muchas oscilaciones ya que estamos llegando al limite de valores permitidos para k.
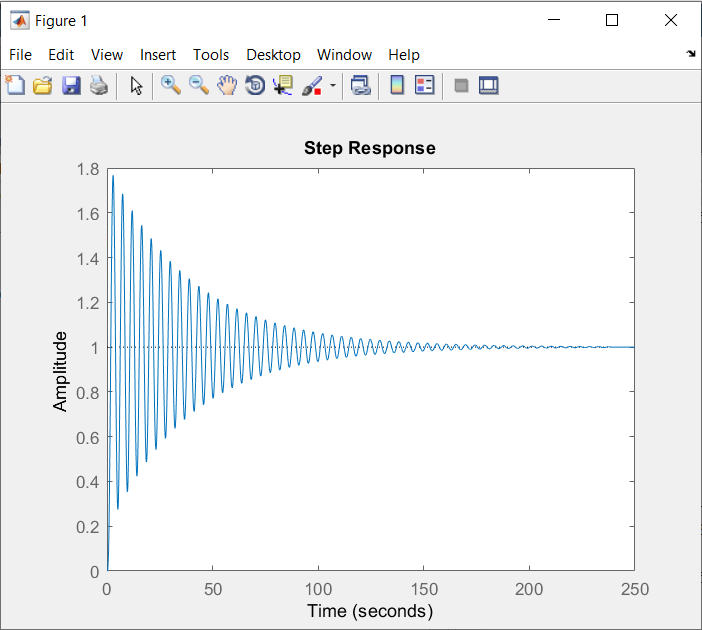
\(fig.\;7\)
En la \(fig.\;7\) podemos ver la gráfica cuando la entrada k es de 17. Como podemos ver en la respuesta, si alcanza a estabilizarse con muchas más oscilaciones ya que estamos llegando al limite de valores permitidos para k.
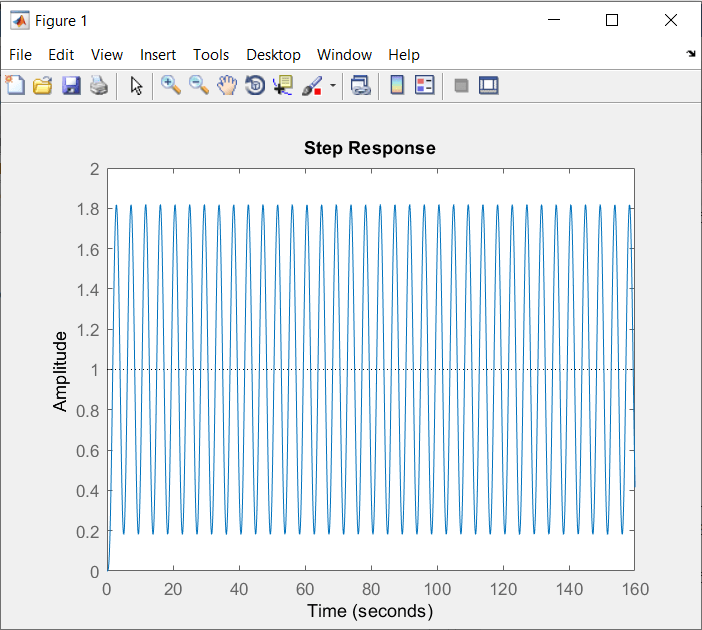
\(fig.\;8\)
En la \(fig.\;8\) podemos ver la gráfica cuando la entrada k es de 18. Como podemos ver en la respuesta, este sistema ya no se estabiliza porque estamos justo en el límite.
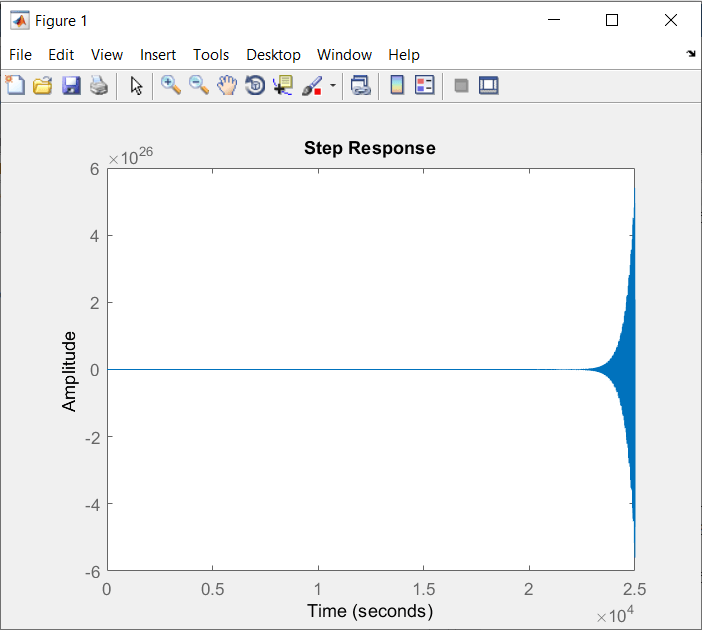
\(fig.\;9\)
En la \(fig.\;9\) podemos ver la gráfica cuando la entrada k es de 18.1. Como podemos ver en la respuesta, este sistema más bien se desestabiliza y a penas nos pasamos por un valor de .1, esto para demostrar lo que ya habiamos establecido de antemano.

